Golangで主成分分析する - 逆さまにした

前回の記事では、多次元正規分布から乱数を生成する方法を書きました。今回は、このデータを使って主成分分析（PCA）を行っていきます。

PCAの詳細については、書籍や他の記事などで十分存在していると思うので、そちらを探してみてください。分散を最大化する方向に軸を取るのか、射影誤差の最小化を行うのかなど複数の解釈が同じ数式に帰着するのも面白いですね。結局は、共分散行列の固有値問題に帰着するのですが。

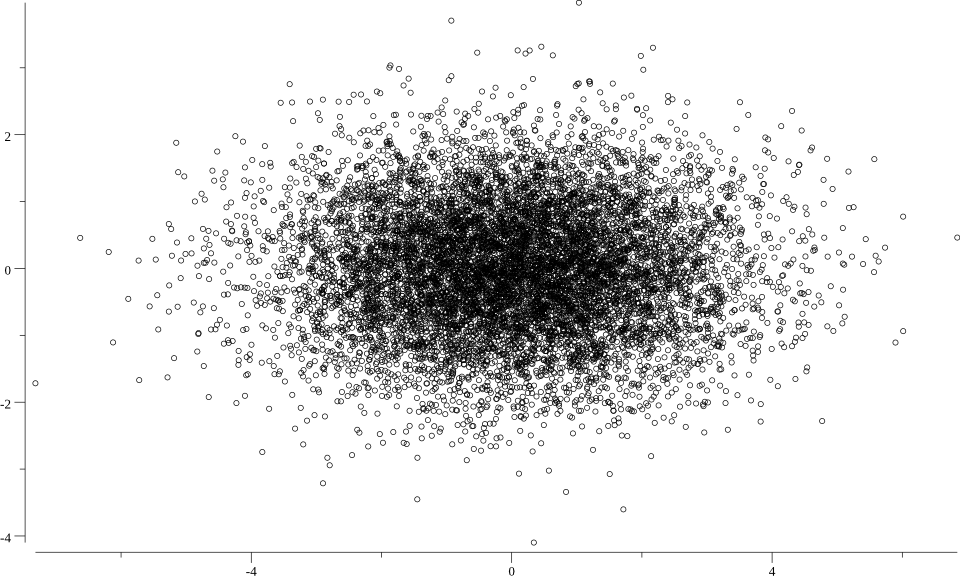
まず、今回の対象データですが、 $\Sigma = \begin{bmatrix} 3.0 \ \ 0.5 \\ 0.5 \ \ 1.0 \end{bmatrix}$ の共分散行列を用いて生成した擬似乱数(2次元×10000個)を使用します。散布図を書くと以下のようになります。

f:id:cipepser:20171030224226p:plain

Golangのstatパッケージでは、PCAを行ってくれるPrincipalComponentsメソッドがあるので、こちらを利用します。

コード

まず擬似乱数の生成です。のちほど使うPrincipalComponentsの引数がmat.Matrixなので、 mat.NewDenseで生成した*mat.Dense型のyに乱数を格納していきます。ちなみに*mat.Dense型はmat.Matrix型のinterfaceを満たします。

y := mat.NewDense(N, d, nil)
for i := 0; i < N; i++ {
  rnd, _ := MultiNorm(mat.NewVecDense(d, []float64{0.0, 0.0}),
    mat.NewSymDense(d, []float64{3.0, 0.5, 0.5, 1.0}),
  )

  y.SetRow(i, mat.Col(nil, 0, rnd))
}

次にPCAの実行です。stat.PC型がPCA用の型となります。

var pc stat.PC
ok := pc.PrincipalComponents(y, nil)

PCAのあとはデータを射影していきます。次元削減を目的とする場合はkで残したい次元数を指定できます。

k := 2
var proj mat.Dense
proj.Mul(y, pc.VectorsTo(nil).Slice(0, d, 0, k))

以上をまとめたコード全体は次のようになります。

giste8f284fa0ed27fa4802ebe0867a795aa

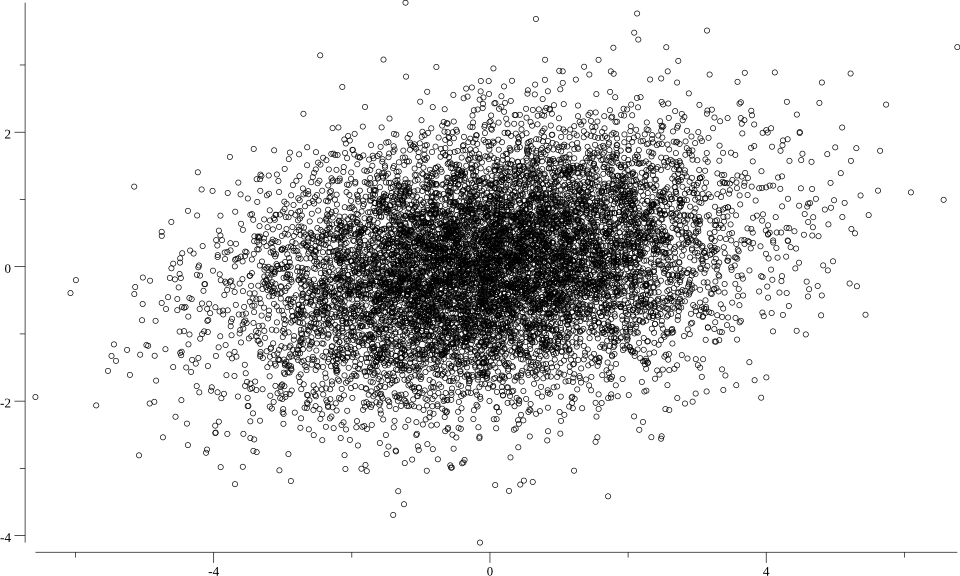
PCA後の散布図は以下のようになりました。

f:id:cipepser:20171030224230p:plain

コード

References