Golangでロジスティック回帰

技評連載の機械学習はじめようを拝見したので、Golangでロジスティック回帰を実装してみます。

イメージしやすいように結果の散布図を先に載せます。赤と青がそれぞれ正解ラベルを表しており、緑色の実践が学習した判別境界です。

f:id:cipepser:20170921224958p:plain

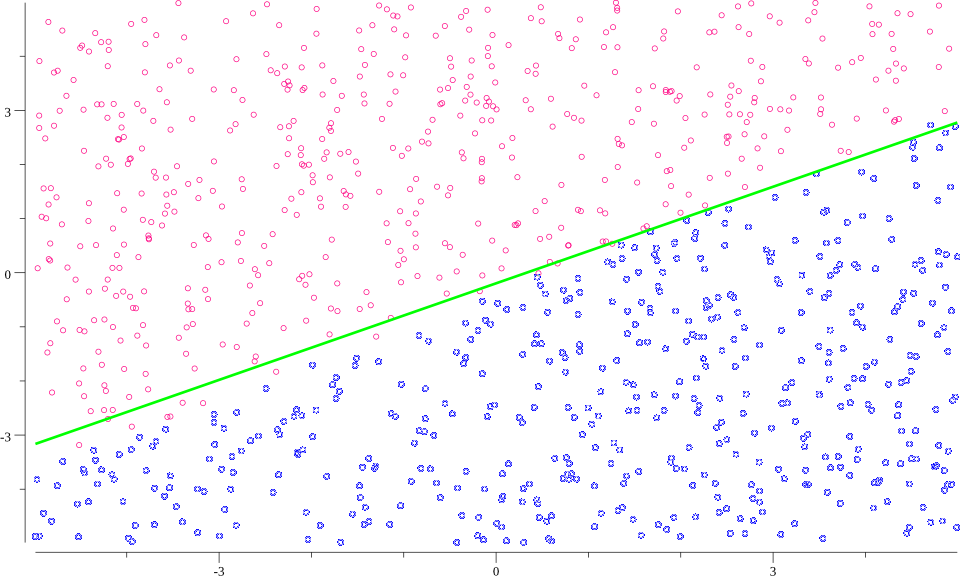
問題設定

以下のように2次元平面上で、一様乱数を生成します。

// テストデータの用意
rand.Seed(time.Now().UnixNano())

x1 := make([]float64, N)
x2 := make([]float64, N)
for i := 0; i < N; i++ {
  x1[i] = 10*rand.Float64() - 5
  x2[i] = 10*rand.Float64() - 5
}

直線 $2x_1+3x_2-1 = 0$ を境界として、生成した乱数に対して、

$2x_1+3x_2-1 \geq 0$ : $t_n = 1$ ,

$2x_1+3x_2-1 \lt 0$ : $t_n = 0$

とラベル付けします。

境界線である直線は、特徴ベクトル $\boldsymbol{x} = [1, x_1, x_2]^T$ と学習したい重み $\boldsymbol{w} = [w_0, w_1, w_2]^T$ を用いて、 $\boldsymbol{w}^T \boldsymbol{x} = 0$ と書けます。直線 $2x_1+3x_2-1 = 0$ なので $\boldsymbol{w} = [w_0, w_1, w_2]^T = [-1, 2, 3]^T$ に近づくことを期待して、 $\boldsymbol{w} = [w_0, w_1, w_2]^T$ を学習するのが目標となります。

方針

式の導出などは機械学習はじめように書かれているため、詳細はそちらを見ていただくとして、 $\boldsymbol{w} = [w_0, w_1, w_2]^T$ を学習するためには、結局、以下を実装すればよいことになります。

$\boldsymbol{w}_{i+1} = \boldsymbol{w}_{i} - \eta \cdot \Bigl(\sigma\bigl( \boldsymbol{w}_{i}^T \phi(\boldsymbol{x}_{n}) \bigr) - t_{n} \Bigr)\phi(\boldsymbol{x}_{n})$

ここで $\eta$ は学習率、 $\sigma(\cdot)$ はシグモイド関数です。

また特徴量は、元データが線形分離可能であることからも、特徴ベクトル $\phi(\boldsymbol{x}) = \boldsymbol{x} = [1, x_1, x_2]^T$ とすれば十分でしょう。第1成分の1はいわゆる切片を表しています。

実装

実装は以下のようになりました。結果を図示するためにgonum/plotを使っています。なのでちょっとコードは長いです。行列やベクトルも同じくgonumのgonum/matを使っています。ちなみにgonum/matrixは既にメンテナンスされておらず、今回用いたgonum/matに移行しているようです。教師データとテストデータはそれぞれ1000個ずつにしています。

giste98445af5552e366cfcb57e81722a0c2

結果

学習した重み\boldsymbol{w}と、教師データ/テストデータを判別した結果は以下です。

// 学習結果
// 参考) 真値: [-1, 2, 3]
&{{1 [-0.5416022992823583 1.6422051384123924 -2.760912629909472]} 3}

// 判別結果
training data:  0.986
new data:  0.982

判別はシグモイド関数の値が0.5を境界として行っています。false positive/negativeをどれくらい許容できる/できないでチューニングも可能です。

結果を見る限り、ある程度は真値に近い値になっていますね。判別結果も新たに生成したデータであっても教師データと同程度の判別率を達成できているのがわかります。

感想

Golangで実装したかったので実装してみましたが、gonum/matのようなパッケージを使うと[]float64からmat.VecDense型への変換などもあって、さくっと書くには少し面倒ですね。そこら辺は動的型付けの言語のほうがよさそうです。

あとは、ロジスティック回帰の理解があやふやだったので、実装してある程度整理できたのでよかったです。特徴量の設計によって非線形の分布に対しても、うまく線形分離可能な空間に飛ばせればロジスティック回帰でかなりの精度が出そうですね。その関数を探すのが大変ですが。。。

逆さまにした

Golangでロジスティック回帰

問題設定

方針

実装

結果

感想

References